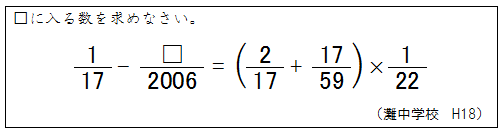
例年、1月から2月かけて行われる中学入試。最近はその時期になると、いわゆる”有名進学校”の難問がネットでも話題になるようです。

さすが有名な学校は違うな、という率直に感嘆する声がある一方で、こんな難しい問題を小学生に解かせるなんて、という批判の声もあります。小学生に難しい問題を解かせることに賛否両論はあっていいと思いますが、しかし、こういった学校は別に小学生をいじめたくて難しい問題を出題するわけではありません。

中学受験に詳しくない人にも名前を知られているような学校はいくつかありますが、特にそういう学校は、どういう生徒に来て欲しいか、という明確なイメージがあります。そして、そういう子たちが、というより、そういう子たちだけが解けるような問題を出しているのです。

たとえば、私の母校でもある灘中学校は、日本一中学入試の算数が難しい学校です。この学校の入試は2日にわけて行われますが、算数も、1日目と2日目の両方にそれぞれあります。そして、1日目は13題前後の1問1答式、2日目は逆に大問5問の記述式、というまったく毛色の違う2種類の算数のテストを受験生に課すのです。

この灘中学校が生徒として欲しがっている人材は明確で、言ってみれば”理系のエキスパート“です。1日目では、短時間で勘所を見抜くセンスを問われ、2日目はじっくり丁寧に考える思考力や遂行力が問われます。要するにこの学校は、センスもあって、粘り強い思考もできる子どもがほしいです、なんて贅沢なことを堂々と宣言しているわけです。（しかし、それこそ日本全国からそういう子どもたちが集まってくるので、そうそう無茶な要求でもなかったりするのが恐ろしいところです。かく言う私も、その”最強”感に憧れて灘中を目指した一人ですが。）

中学校がなぜそういう子どもたちを求めるか、というと、もちろん進学実績を出すため、ということもあるでしょう。しかしそれより、入学後のカリキュラムの問題も大きいです。

これは灘中学に限った話ではありませんが、いわゆる有名進学校では、中学1年生の間に中学内容の数学を終わらせてしまう、と言われています（実際には中2の頭くらいまでかかりますが）。

それじゃあ、中学校の間に高校までの範囲が終わっちゃうんじゃないの、後は何をするの？と思うかもしれません。しかしこれは少し予想と違って、実際には高校の範囲の学習を4年かけておこないます。つまり、中学内容を駆け足で終らせ、それによって、高校内容をじっくり学習するための時間の余裕を作るのです。

中学くらいまではなんとかついていっていたけど、高校に入ったら数学がわからなくなった、という人も多いと思います。それは言ってみれば当然の話で、高校内容の数学はそもそもとても難しいです。個人的には、3年間学校で習ったくらいで理解できるものではないと思っています。だからこそ、進学校では可能な限り多くの時間をその学習のために確保したいですし、そのために中学内容を手早く終わらせてしまいたいのです。そして、そういうカリキュラムを組むために、中学内容の数学くらいまでは、すでにある程度身につけている子どもがほしいのです。

もちろん、だからといって、単に”中学内容を先取りしている子ども”がほしいわけではありません。
冒頭の”計算問題”を見て下さい。「＝（イコール）」の左側だけでなく、右側にも式があります。この形は何を意識しているかというと、「方程式」を想定しているわけです。

つまり、方程式の解ける子どもがほしい、と言っても、単純に「x」や「y」が使えるかどうかではなく、「複雑な方程式を解ききる技術」を実際に持っているかどうか、を見ているのです。（ちなみに、冒頭の問題は、灘中学校の1日目の1番目のもので、例年こういった計算問題が出題されます。計算問題なので時間をかければ解くことはできますが、あまり時間をかけると他の問題に響くため、手早く正確に解くことが求められています。答えは81です。）

中学入試で数学ができるかどうかを見ている、ということは、中学入試の問題には数学の基礎的な部分のエッセンスが詰まっている、ということでもあります。そういった意味では、数学を学習する上で、中学入試の問題を解く、というのは、ひとつ重要な過程だと思います。もちろん、すべての子どもが中学受験をする必要はないでしょう。12歳の時点でそれができる子どもばかりだとも思いません。しかし、どこかの段階で中学入試の問題にふれておくことは、数学を受け入れる下地を作るためのいいトレーニングになると思うのです。

いつの間にか数学についていけなくなった人や、これから数学を学びなおしてみたい人は、まず中学入試の問題に挑戦してみるのもいいかもしれません。

小田敏弘（おだ・としひろ）　数理学習研究所　所長
灘中・高、東大卒。「学校のテストのための勉強」「受験のための勉強」「実生活で役立つ勉強」「趣味としての勉強」「学問としての勉強」など、様々な数理学習（算数・数学の学習）へのニーズがある現状に対して、そういった個々の場面にとらわれない、すべてに通底するものがあるはず、と考えている。現在はその”本質的な数理学習”を追究し、学習者に提供するべく、様々な活動を展開している。ホームページ：http://kurotake.net/

主な著書：
「できる子どもは知っている　本当の算数力」
算数の「できる子ども」と「できない子ども」は何が違うのか。　一般的には漠然と語られている “算数のセンス”。その実体を、具体的に、かつ詳細に解説した本。

「文の会式　東大脳さんすうドリル」 「文の会式　東大脳さんすうドリル　図形編」（3月20日発売）
“センス”を磨くために必要なことは、計算や図形のさまざまな面と触れ合い、それらに対するイメージを豊かにすること。　本ドリルは、パズルなどを通じて数や図形との”ふれあい”を増やし、そういったものに対する豊かな感性を育てることが目的。小学生向けのドリルだが、脳トレ目的でハマる大人も。